
Binary Search (이분탐색) 이란?
"정렬"되어 있는 배열에서 특정 값의 위치를 찾는 탐색알고리즘이다.
탐색하는 배열을 둘로 나누고 찾고자하는 값이 존재하는 영역만 탐색하기 때문에 전체를 탐색하는 경우보다 당연히 빠르게 찾을 수 있다.

과정
내가 찾고자하는 값을 '타겟'이라고 하자.
이분탐색은 주로 배열에서 타겟의 위치(인덱스)를 찾고자 할 때 많이 사용된다.
1. 탐색할 배열을 정렬한다.
2. 탐색할 영역의 중앙값( = (시작점 + 끝점)/2)이 타겟과 비교한다.
2-1. 중앙값이 타겟과 같다면 중앙값의 위치를 반환하고 탐색을 종료한다.
2-2. 타겟이 중앙값보다 작다면 다음엔 중앙값을 기준으로 왼쪽을 탐색해야하므로 끝점을 중앙점 -1로 이동한다.
2-3. 타겟이 중앙값보다 크다면 다음엔 중앙값을 기준으로 오른쪽으로 탐색해야하므로 시작점을 중앙점 +1로 이동한다.
3. 시작점이 끝점보다 커질때까지 2번을 반복한다.

위의 배열에서 값이 7인 위치를 이분탐색을 이용하여 찾아보자.
1. 탐색할 배열을 정렬한다.
정렬은 시간복잡도에 맞게 적절하게 사용하면 될 것이다.
2. 탐색할 영역의 중앙값( = (시작점 + 끝점)/2)이 타겟과 비교한다.
2-1. 중앙값이 타겟과 같다면 중앙값의 위치를 반환하고 탐색을 종료한다.
2-2. 타겟이 중앙값보다 작다면 다음엔 중앙값을 기준으로 왼쪽을 탐색해야하므로 끝점을 중앙점 -1로 이동한다.
2-3. 타겟이 중앙값보다 크다면 다음엔 중앙값을 기준으로 오른쪽으로 탐색해야하므로 시작점을 중앙점 +1로 이동한다.

중앙점의 값 6과 타겟 7과 비교해보자
2-1 중앙값과 타겟의 값이 6, 7로 다름
타겟(7)이 중앙점의 값(6)보다 크므로 2-3경우에 해당되며 중앙점 기준 오른쪽을 탐색해야한다.
시작점을 중앙점 +1로 이동시킨후 다시 중앙점을 잡아보면.

위와 같다.
3. 시작점이 끝점보다 커질때까지 2번을 반복한다.
2번 과정을 반복해보면
중앙점의 값 9과 타겟 7과 비교해보자
2-1 중앙값과 타겟의 값이 9, 7로 다름
타겟(7)이 중앙점의 값(9)보다 작으므로 2-2경우에 해당되며 중앙점 기준 왼쪽쪽을 탐색해야한다.
끝점을 중앙점 -1로 이동시킨후 다시 중앙점을 잡아보면.

위와 같다.
2번 과정을 반복해보면
중앙점의 값 7과 타겟 7과 비교해보자
2-1 중앙값과 타겟의 값이 7과 7로 같으므로 중앙점위치 4를 반환한 후 종료한다.
특징
1. 시간복잡도 : 최선 : O(1), 최악, 평균 : O(log N)
탐색해야할 배열의 크기가 N 이라하면, 첫번째 탐색 후에 탐색해야할 영역이 절반으로 줄어들게 된어

으로 탐색해야할 영역의 크기가 된다.
두번째 탐색후 또 절반으로 줄어들게 되어

세번째 탐색후에는 또 절반으로 줄어들게 되어

K 번의 시행 후에는?

크기만 남게 된다.
이렇게 계속해서 탐색을 반복하다보면 탐색이 끝나는 시점에는 찾고자하는 타겟 1개가 남게 된다.

따라서 위와 같이 표기 할수 있다.
이 때, 양 변에

을 곱해주면

마지막으로 양 변에 2를 밑으로 하는 로그를 취해주면,
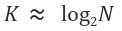
가 된다.
따라서 자료의 갯수 N에 따른 시행 횟수는

가 되고 시간 복잡도는 Big O 표기법으로
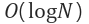
로 나타낼 수 있다.
2. 정렬된 배열에서만 사용가능하다.
코드
1. 같은 값이 중복해서 들어오지 않는 경우 (즉, lower bound, upper bound를 적용하지 않았을때)
package algo;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class BinarySearch {
static int goal;
static int idx;
static int arr[] = {65,1,4,34,87,91,6,9,12,71,7,8,78};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 입력된 값의 위치를 반환
goal = Integer.parseInt(br.readLine());
//이분탐색은 정렬된 상태에서 탐색
Arrays.sort(arr);
System.out.println(Arrays.toString(arr));
BinarySearch1(0, arr.length-1);
System.out.println(idx);
BinarySearch2(0, arr.length-1);
System.out.println(idx);
}
// 재귀로 구현한 이분탐색
static void BinarySearch1(int start, int end) {
if(start > end) {
return ;
}
int mid = (start+end) / 2;
if(arr[mid] == goal) {
idx = mid;
return;
}else if(goal < arr[mid]) {
BinarySearch1(start, mid-1);
}else if(arr[mid] < goal) {
BinarySearch1(mid+1, end);
}
}
// 반복문으로 구현한 이분탐색
static void BinarySearch2(int start, int end) {
int mid ;
while (start <= end){
mid = (start + end )/2;
if(arr[mid] == goal){
idx = mid;
return;
}else if(arr[mid] < goal){
start = mid +1;
}else if(arr[mid] > goal) {
end = mid - 1;
}
}
}
}
Lower Bound 와 Upper Bound
Lower Bound와 Upper Bound 는 탐색할 배열에 같은 값이 2개 이상 존재할 경우 타겟을 어떤 걸로 할지 정하는 기준이다.
즉 1 2 4 4 4 5 5 6 이라는 배열이 있을 때 찾고하자 하는 값이 4라면 타겟을 가장 왼쪽에 존재하는 인덱스가 2인 4로 정할지, 가장 오른쪽에 존재하는 4의 다음 인덱스인 5로 정할지 기준을 정하는 것이다.
Lower Bound 는 가장 왼쪽에 위치한 타겟을 의미하며
Upper Bound 는 가장 오른쪽에 위치한 타겟의 다음 위치를 의미한다.

'Algorithm > 알고리즘 정리' 카테고리의 다른 글
| [알고리즘 정리] Merge Sort ( 병합정렬 ) - O(NlogN), 추가메모리, Stable (0) | 2024.01.20 |
|---|---|
| [알고리즘 정리] Topology Sort ( 위상 정렬 ) - O(V+E), 순서가 정해져 있는 작업, 여러 답이 존재 (0) | 2023.06.26 |
| [알고리즘 정리] Counting Sort ( 계수 정렬 ) - O(N+k), 추가 메모리, Stable (0) | 2023.06.25 |
| 아스키 코드(ASCII) 잘 쓰이는 거 모음 (3) | 2023.06.21 |