
Topology Sort (위상 정렬) 이란?
위상 정렬은 사이클이 없는 방향그래프 (DAG: Directed Acyclic Graph)에서 각 정점의 선후를 위배하지 않고 정렬하는 알고리즘이다.
정해진 선후만 위배하지 않으면 되기 때문에 정렬된 결과가 여러개가 나올 수 있다.
작업의 순서가 정해져 있을때 일직선의 순서를 찾는 알고리즘이라고 생각하면 편하다.
ex ) 집도착 → 손발 씻기 → 밥먹기 → 설거지하기 → 과제하기 → 유튜브 보기 → 잠자기
이때 주어진 엣지의 방향만 지키면 된다.
만약
기초수학 → 물리
기초수학 → 화학
이라는 선후가 주어진다면
기초수학→물리 → 화학
도 괜찮고
기초 수학 →화학 →물리
도 괜찮다
같이보면 좋은 백준 문제
과정
위상정렬을 구현하기 위해서는 "진입차수(InDegree)"가 필요하다.
진입 차수란 특정 정점노드로 들어오는 간선의 개수를 의미한다.
즉 1번, 4번 노드가 2번 노드로 간선이 향하고 있다면 2번 노드로 들어오는 간선의 개수는 총 2개 이므로 진입차수는 2가 된다.
위상 정렬은 큐 또는 스택, DFS로 구현이 가능하다.
나는 큐로 구현 해보았다.
- 진입차수 배열 만들기
- 시작점을 큐에 삽입
- 큐에서 원소를 그 노드와 꺼내 연결된 모든 간선을 제거
- 간선제거 이후 들어오는 간선의 개수가 0인 정점을 큐에 삽입
- 큐가 빌때까지 2 ~ 3번 과정을 반복
- 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재, 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상정렬의 결과

과정에 따라서 그래프를 일직선으로 정렬해보자.
1.시작점을 큐에 삽입
시작점은 정점에 들어노는 간선이 없는 정점들을 시작점으로 한다.
정점에 들어오는 간선이 있는지 없는지를 판별하기 위해서는 진입차수 배열(InDegree)를 만들어야한다.

이 그래프에서는 Indegree 가 0인 1번과 3번이 시작정점으로 큐에 삽입되게 된다.

이때 방문 배열과 큐의 상태는 위와 같다.
2. 큐에서 원소를 그 노드와 꺼내 연결된 모든 간선을 제거
이제 큐에서 원소들을 한개씩 빼서 그 정점과 연결된 간선들을 제거 할 것이다.
큐에서 먼저 나오는 정점은 1번이다.

간선을 그래프에서 그림처럼 제거했다 "치고"!
진입차수가 변한 노드들을 있기 때문에 이를 갱신 해주어야 한다

1번 노드에 연결된 2번으로 향하는 간선과 4번으로 향하는 간선이 제거 되었기 때문에
2번의 진입차수는 1로 / 4번의 진입차수는 0으로 갱신되었다.
3. 간선제거 이후 들어오는 간선의 개수가 0인 정점을 큐에 삽입
변화된 진입차수를 가지고서 방문하지 않은, 즉 큐에 넣지 않은 노드 이며 진입차수가 0인 노드를 큐에 삽입한다.
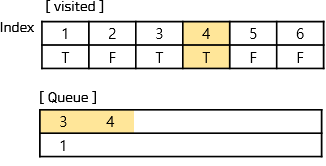
이때 방문 배열과 큐의 상태는 위와 같다.
큐의 두번째 줄은 큐에서 나온 순서 즉 정렬된 상태이다.
4. 큐가 빌때까지 2 ~ 3번 과정을 반복







마지막에는 큐가 비게 되어 반복문을 탈출하고 나온 결과는 1 , 3, 4, 2, 5, 6으로 출력되게 된다.
5. 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재, 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상정렬의 결과
위 경우 모든 원소를 방문하고 반복문을 탈출하게 되어 사이클이 존재하지 않는다는 것을 알 수 있다.
이유는 사이클을 돌게 되면 사이클에 속해 있는 정점들의 진입차수가 무조건 1씩 남게 되기 때문에
큐에 들어갈 수 없다.
특징
1. 시간복잡도 : 정점의 개수를 V, 간선의 개수를 E라고 할때, 최선 O(V + E) , 최악 O(N+K)
O(V) => 차례대로 노드를 확인
O(E) => 방문 중인 노드에서 출발하는 개수의 총
2. 사이클이 없는 방향그래프(DAG)에서만 적용 가능
3. 선후가 정해져 있는 정렬에서 사용가능
4. 정렬된 답이 여러개로 존재 할 수 있다.
5. 사이클이 존재하는지 판단할 수 있다.
모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다.
사이클에 포함된 원소 중 어떠한 원소도 큐에 들어가지 못한다.
코드
package algo;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class TopologySort2 {
static int V; //정점의 개수
static int E; //간선의 개수
static ArrayList<Integer> [] graph;
static int[] InDegree; // 진입차수 기록
static Queue<Integer> q;
static boolean[] visited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
graph = new ArrayList [V+1]; //노드번호 1~6까지 이므로 인덱스번호 1~6까지 사용
for (int i = 0; i < V+1; i++) {
graph[i] = new ArrayList<>();
}
InDegree = new int[V+1];//각 정점에서 들어오는 간선이 몇개인지 저장하는 배열
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
graph[start].add(end);
InDegree[end]++; //진입차수 기록
}
//===========입력
q = new LinkedList<>();
visited= new boolean[V+1];
//1.시작점을 큐에 삽입
for (int i = 1; i < V+1; i++) {
if(InDegree[i] == 0) {
//들어오는 간선이 없으면 그 정점을 시작점으로 하기 위에 큐에 넣는다.
q.add(i); //진입차수가 0인 것을 시작점으로 두기
visited[i] = true;
}
}
//탐색 시작
while (!q.isEmpty()) { //4. 큐가 빌때까지 2 ~ 3번 과정을 반복
int n = q.poll();
//2. n 정점으로부터 나가는 간선들을 제거
for (int v : graph[n]) {
InDegree[v]--;
}
//3. 간선을 제거 후 들어오는 간선이 없는 정점을 다시 큐에 넣기
for (int i = 1; i < InDegree.length; i++) {
if(InDegree[i] == 0 && !visited[i]) {
q.add(i);
visited[i] = true;
}
}
System.out.print(n+" ");
}
//5. 사이클 존재 여부 판단
for (int i = 1; i < V+1; i++) {
if(!visited[i]) {
System.out.println("사이클 존재!!");
break;
}
}
}
}
실행 결과
<input>
6 6
1 2
1 4
2 5
2 6
3 6
4 2
<output>
1 3 4 2 5 6
'Algorithm > 알고리즘 정리' 카테고리의 다른 글
| [알고리즘 정리] Merge Sort ( 병합정렬 ) - O(NlogN), 추가메모리, Stable (0) | 2024.01.20 |
|---|---|
| [알고리즘 정리] Binary Search ( 이분 탐색 ) - O(logN), 탐색알고리즘 (0) | 2023.08.14 |
| [알고리즘 정리] Counting Sort ( 계수 정렬 ) - O(N+k), 추가 메모리, Stable (0) | 2023.06.25 |
| 아스키 코드(ASCII) 잘 쓰이는 거 모음 (3) | 2023.06.21 |