728x90
반응형
[Silver II] 수들의 합 4 - 2015
성능 요약
메모리: 35852 KB, 시간: 312 ms
깨진 부분은 여기에서 확인
🤔접근법
범위 체크 및 시간복잡도 예상
- 1 ≤ N ≤ 200,000
- |K| ≤ 2,000,000,000 (20억)
- $O(N\sqrt N)$ 이하 이어야 한다.
풀이법
❌ 접근 방법. 완탐
- 시작점이 0 ~ N-1 , 끝점이 0 ~ N-1로 두고 가능한 모든 부분 배열을 지정한다. → $O(N^2)$
- 부분 배열을 순회하며 부분합을 구한다. → $O(N)$
- 부분합이 k와 같은지 비교한다.
➡️ 해당 풀이법의 시간 복잡도 : $O(N^3)$
시간복잡도가 너무 커서 시간이 부족하다.
❌ 접근 방법. 누적합
- 누적합 배열($S_n)$을 만든다. → $O(N)$
- $S_b-S_{a-1}$ 모든 부분 배열의 누적합을 구한다. → $O(N^2)$
- 부분배열의 누적합이 k와 같은지 비교한다.
➡️ 해당 풀이법의 시간 복잡도 : $O(N^2)$
⭕ 접근 방법. Map을 이용한 부분 배열의 합의 개수
- 1 ~ N까지 순회하며 누적합을 구한다.
- 현재 누적합에서 K를 만들어 내는 수 를 key로 가지는 map의 요소가 존재한다면 부분합이 K인 부분배열이 있다는 의미이므로 cnt += value
- 현재 누적합을 key로 가지는 map이 존재하면 value에 +1
- 존재하지 않는다면 map에 추가
👇 설명
N = 6이고 K=5일때 아래와 같은 배열이 존재하며 이를 통해 구한 누적합은 아래와 같다.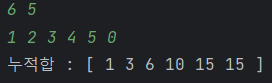
이때 누적합 배열($S_n)$에서 a ~ b까지의 부분 배열의 합은 $S_b-S_{a-1}$ 이렇게 구할 수 있다.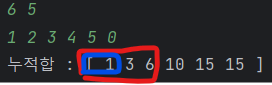
그렇다면 만약 $S_2$ = 6을 탐색하고 있었다면 인덱스 2 이전에서 $S_{a-1}$= 1인 누적합이 존재하는지 판별하면 모든 배열을 돌지 않고도 K와 같은 부분합을 가지는지 알 수 있다.!
우리는 이전에 $S_0$=1 이라는 것을 알 수 있었다.
그래서 $S_2 - S_0 = 5$ 여서 K와 같은 부분합을 가지는 배열이 존재했음 알 수 있다.
그렇다면 우리는 누적합에서 K를 만들어 내는 수 (즉, 위에서 6-1에서 1같은)의 개수를 빠르게 알아내는 방법을 생각해보아야 한다.
key : 누적합으로 나올 수 있는 값 , value : 누적합을 key로 가지는 부분배열의 개수인 Map을 통해 저장하면 누적합을 만들면서 K와 같은 부분합을 가지는 배열의 개수를 알아낼 수 있다.
➡️ 해당 풀이법의 시간 복잡도 : $O(N)$
🤯FAIL
답을 봐서 문제를 푼 경우
- 해결이 되지 않은 부분 : 누적합 배열을 사용해도 시간복잡도가 충분하지 않았다.
- 정답의 로직은 ?
누적합을 순회하며 K를 만들기 위한 수가 정해져 있었고 이 수가 있는지 없는지 판별을 map으로 한다는게 킥이었다.
범위 오류
- 부분합 중 합이 K인 것이 Int 범위를 넘어 갈 수 있다는 것을 생각하지 못하였다.
참고 블로그
👩💻 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.HashMap;
import java.util.StringTokenizer;
public class Main_2015 {
static int N;
static long K;
static long A[];
static long prefixSum[];
static HashMap<Long, Integer> prefixSumCntMap;
static long cnt;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
K = Long.parseLong(st.nextToken());
A = new long[N+1];
prefixSum = new long[N+1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N ; i++) {
A[i] = Long.parseLong(st.nextToken());
}
prefixSumCntMap = new HashMap<>();
prefixSumCntMap.put(0L,1); // prefixSum[i]와 K가 같은 경우
for (int i = 1; i <= N; i++) {
// 누적합 배열
prefixSum[i] = prefixSum[i-1] + A[i];
// K를 만드는 수를 key로 가지는 map이 있다면 value를 반환
// 없다면 0을 반환
cnt += prefixSumCntMap.getOrDefault(prefixSum[i]-K,0);
prefixSumCntMap.put(prefixSum[i], prefixSumCntMap.getOrDefault(prefixSum[i],0)+1);
}
System.out.println(cnt);
}
}반응형
'Algorithm > PS - 백준' 카테고리의 다른 글
| [백준 Java] 3020번 개똥벌레 (0) | 2024.01.13 |
|---|---|
| [백준 Java] 2143번 두 배열의 합 (1) | 2024.01.13 |
| [백준 Java] 2004번 조합 0의 개수(정수론) (0) | 2024.01.09 |
| [백준 Java] 2247번 실질적 약수(정수론) (1) | 2024.01.08 |
| [백준 Java] 23888번 등차수열과 쿼리 (정수론) (1) | 2024.01.08 |
