[SW_2] Meta-heuristic: TSP(외판원문제) - simulated annealing(담금질 기법)

1. Meta-heuristic : 특정 문제에 특화되지 않고 자연에서 영감을 얻은 경험적 방법

• 대표적인 meta-heuristic : Simulated Annealing, Tabu Search, Genetic Algorithms, Ant Colony Optimizatio

 

2. Simulated Annealing(담금질 기법) : 커다란 탐색공간에서 주어진 함수의 전역 최적점(global optimum)에 대

한 훌륭한 근사치를 찾으려고 하는 전역최적화 문제에 대한 일반적인 활률적 휴리스틱 접근 방법이다.  

• 금속의 담금질(annealing) 이란 고체를 녹을때 까지 가열하고 난 후 그것을 완전한 결정체가 될때까지 식히는 물리적인 과정으로 이 과정에서 고체의 자유에너지는 최소화된다. 이런 과정에서 내부의 결함을 없애기 위해 조심스럽게 천천히 냉각시켜야한다.
• 위와 같은 과정에서 생각을 얻어 만든 SA 는 온도를 급속히 낮추면 전역 최적점에 도달할 확률이 적고, 온도를 천천히 낮추면 전역 최적점을 찾을 확률은 높아지지만 많은 반복을 필요로 하므로 시간이 오래 걸리게 된다.

 

3. Local Search 와 SA

SA는 local search 를 개선한 방법론이다.

• local search
  1. 초기해를 만든다
  2. 현재의 해를  랜덤하게 변화시킨다.
  3. 새로운 해가 원래 해 보다 좋다면 바꾸고, 그렇지 않다면 무시한다.
  4. 2~3  과정을 적당히 반복한다.
• SA
  
  1. 초기해를 만든다
  2. 현재의 해를  랜덤하게 변화시킨다.
  3. 새로운 해가 원래 해 보다 좋다면 바꾸고, 그렇지 않다면 일정한 확률로 바꾼다.
  4. 2~3  과정을 적당히 반복한다.
• 두 방법의 차이는 3번으로 SA는 원래 해 보다 좋지 못한 해도 일정한 확률로 바꾸어 local optimum에 빠져 나올 수 있도록 장치를 두었다.
• 일정한 확률를 지정하기 위하여 "온도"라는 개념을 두었고 처음에는 좋지 못할 해로 바꿀 확률을 크게 두고 점점 그 확률을 조금씩 줄여서 0이 되도록한 후 0이 되면 SA 탐색을 마치게 된다. 

 

4. SA 프로세스

SA step 1. 매개변수 초기화 및 초기 함수 세팅

• 초기 온도(T_0) 설정 
• 냉각 온도(delta) 설정 (몇 도 씩 떨어뜨릴지)
• 최종 온도(T_final) 설정 (온도가 몇 도가 되면 종료할지)
• 최대 런타임(cutoffTime) 설정
•  
• 초기해(cur_path) 설정 (TSP 문제에서의 해는 최소 비용의 경로를 의미한다.)
• 현재해를  초기해로 설정
• 현재 해에 대한 비용(cur_dis)를 초기 해에 대한 비용로 설정 (TSP 문제에서는 최소 비용경로의 비용을 의미한다.)
• 현재 온도(cur_t)를 초기 온도로 설정
• 가장 좋은 해를 현재 해로 설정
• 가장 좋은 비용을 현재 해의 비용으로 설정

SA step 2. neighbor solution 찾기

• 기존의 솔루션을 적당히 변경하여 조금 다른 솔루션을 만들어 현재해를 변화시켜 새로운 해를 만든다.

SA step 3. 새로운 해에 대해 확인하기

• 새로운 해가 원래해보다 좋다면 바꾸기
• 새로운 해가 원래해보다 좋지 않다면 볼츠만 상수를 이용한 기준에 따라 랜덤한 값이 그것보다 작다면 새로운 해로 바꾼다. 
• 새로 바꾼해가 가장 좋은 해보다 좋다면 가장 좋은 해로 변경한다.

SA step 4. 반복조건 확인하기

• 현재 온도에서 냉각 온도를 빼고 현재온도로 설정한다.
• 현재 온도가 최종 온도보다 작거나 현재 런타임이 최대 런타임보다 크다면 반복을 중단한다.
• 이를 만족하지 않으면 2~3번의 과정을 반복한다.

 

---

 

 

지난 글에서는 greedy 방법을 이용한 TSP 문제를 해결해보았지만 global optimum을 찾기는 힘들었다.

이번 글에서는 SA 탐색방법을 이용하여 TSP 문제를 해결해보고자 한다.

TSP 문제에 대한 설명과 heuristic에 관한 설명은 지난 글을 참고

지난 글 - 2022.09.15 - [SW 부트캠프 SW_2] - [SW_2] Heuristic: a routing problem(TSP, 외판원문제) - Greedy

 

문제는 지난 글과 같다.

 

문제 : 100개의 도시 정보가 첨부 파일(“Input_data.csv”)에 있다. 이 파일은 도시별 일련변호(NO.), x좌표
(XCOORD.), y좌표(YCOORD.) 등의 정보를 포함하고 있다. 모든 도시를 여행하고 출발지(0번 도시)
로 돌아오는 경로(route)와 거리(distance)를 구하시오. 단, 두 도시(A, B) 사이의 거리(D)는
Euclidean Distance 방식으로 계산한다(아래 수식 참고).

Input_data.csv

0.00MB

해결 조건 : SA 기반으로 문제를 해결하여 가장 좋은 해의 비용이 510 이하로 하여 답이 개선되는 과정을 가시적으로 표현

정답 예)

풀이 : 

1. 매개변수 초기화 및 초기 함수 세팅

• 초기 온도(T_0) 100000로 설정
• 냉각 온도(delta) 0.999로 설정
• 최종 온도(T_final)  1e-8로 설정 
• 최대 런타임(cutoffTime) 100으로 설정(했지만 사용안함)

2. neighbor solution 찾기 (함수명 solution())

• 기존 솔루션을 변화시키는 방법으로는 기존의 경로에서 부분을 추출하여 뒤집은 후 다시 넣었다.
• 부분을 추출할때 기준은 랜덤하게 하였다.

3. 새로운 해에 대해 확인하기

 

• 새로운 해가 원래해보다 좋다면 바꾸기

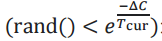
• 새로운 해가 원래해보다 클때 랜덤한 수가 자연상수 e 의 (-새로운 경로의 거리와 기존 경로의 거리의 차이/현재온도) 제곱 보다 작으면 새로운 해로 변경하도록 기준을 정하였다.
• -새로운 경로의 거리와 기존 경로의 거리의 차이 = -ΔC
• 현재온도 = Tcur
• ΔC가 작을수록 채택 확률이 높아지며 Tcur 클수록 채택 확률이 높아진다.
•  
• random.random() < math.exp(-abs(c/cur_t)):

 

4. 반복조건 확인하기

 

코드 :

import pandas as pd
import math
import random
import matplotlib.pyplot as plt
import time 


df = pd.read_csv('Input_data.csv')

mat=[]
for i in range(0,100):
    mat.append([df.loc[i][1], df.loc[i][2]])

def dis_solution(start, end) :
  a = start[0] - end[0]
  b = start[1] - end[1]
  d = math.sqrt((a * a) + (b * b))
  return d


def random_path():
  path=[0]
  path1 = [i for i in range(1,100)]
  random.shuffle(path1)
  path = path + path1
  path.append(0)
  return path


def dis(path):
  sum =0
  start=0
  for i in range(0,100):
    start = mat[path[i]]
    end = mat[path[i+1]]
    d = dis_solution(start,end)
    sum= sum+d
  return sum


def solution(cur_path):  #neighbor soluion 만들기
  ran1 = random.randrange(0,99)
  ran2 = random.randrange(0,99)

  if ran1>ran2:
    ran1, ran2 = ran2, ran1

  str1= cur_path[:ran1]
  str2=cur_path[ran1:ran2]
  str3=cur_path[ran2:]
  str2.reverse()
  path=str1+str2+str3

  return path  #비슷한 최소 경로의 거리


# 1. 매개변수 초기화 및 초기 함수 세팅
T_0 = 100000
delta = 0.999 #t_0에서 얼마나 떨어뜨릴지
T_final =1e-8  #t_0이 1e-8 이 되면 실행 종료
cutoffTime = 100  #최대 런타임

cur_path = random_path()
cur_dis = dis(cur_path)
cur_t = T_0

best_path = cur_path
best_dis=cur_dis
cur_dis_list=[cur_dis]
best_dis_list=[best_dis]
# print(cur_path)


while 1:
# 2. neighbor solution 찾기 (함수명 solution())
  new_path = solution(cur_path)
  new_dis=dis(new_path)
  # 3. 새로운 해에 대해 확인하기
  if new_dis < cur_dis:
    cur_path= new_path
    cur_dis=new_dis
  else:
    c = new_dis - cur_dis
    if random.random() < math.exp(-abs(c/cur_t)):
      cur_path=new_path
      cur_dis=new_dis
  if dis(cur_path) < best_dis:
    best_path=cur_path
    best_dis=dis(cur_path)
  # 4. 반복조건 확인하기
  cur_t*=delta
  cur_dis_list.append(cur_dis)
  best_dis_list.append(best_dis)
  if cur_t < T_final:
    break;
  

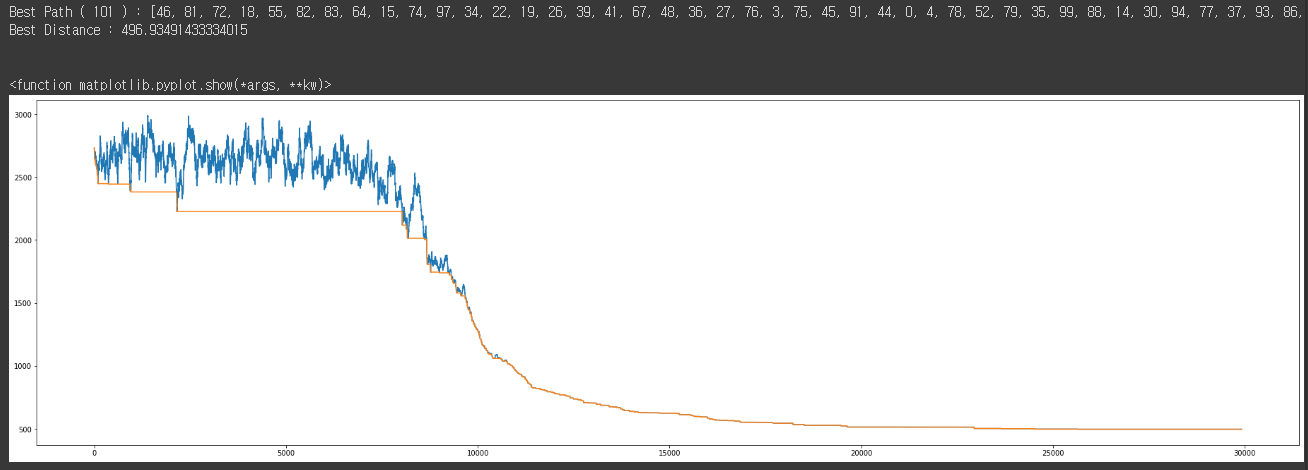
print("Best Path (",len(best_path),") :", best_path)
print("Best Distance :", best_dis)
print()
print()
plt.rcParams['figure.figsize'] = [32, 9] 
plt.plot(cur_dis_list)
plt.plot(best_dis_list)
plt.show

 

결과 : 실행결과를 통하여 가장 좋은해의 비용이 496인 것을 확인할 수 있다.